Ibload486

1. Fieldline Pro Series
2. Fieldline Range Bag

A field line is a graphical visual aid for visualizing vector fields. It consists of a directed line which is tangent to the field vector at each point along its length.^[1][2] A diagram showing a representative set of neighboring field lines is a common way of depicting a vector field in scientific and mathematical literature; this is called a field line diagram. They are used to show electric fields, magnetic fields, and gravitational fields among many other types. In fluid mechanics field lines showing the velocity field of a fluid flow are called streamlines.

Definition and description[edit]

Microsoft Windows Screensaver files such as FieldLines.scr utilize the SCR file extension. This file is considered a Win32 EXE (Microsoft Windows Screensaver) file, and was first created by TGT Soft for the Style XP 3.19 software package. The initial introduction of FieldLines.scr released in Style XP 3.19 was for Windows 10 on. (E20) Faraday and his 'Lines of Force' In our homes, cars, communications, computing and machinery, electric currents are are usually channeled by insulation wrapped around wires and boundaries. Today, Fieldline® is a worldwide hunting gear manufacturer and distributor and although they no longer have their department stores, they still continue in their longtime retail commitment to. Electric field lines in 3D The electric field exists in 3-dimensional space. Below you can explore 3D drawings of the electric field lines of two charges. You can change the magnitude (arb. Units), sign, and position (arb. Units) of the each charge.

A vector field defines a direction and magnitude at each point in space. A field line for that vector field may be constructed by starting at a point and tracing a line through space that follows the direction of the vector field, by making the field line tangent to the field vector at each point.^[3][2][1] A field line is usually shown as a directed line segment, with an arrow indicating the direction of the vector field. For two-dimensional fields the field lines are plane curves, and most field line diagrams are of this type. Since at each point where it is nonzero and finite the vector field has a unique direction, field lines can never intersect, so there is exactly one field line passing through each point at which the vector field is nonzero and finite.^[3][2] Points where the field is zero or infinite have no field line through them, since direction cannot be defined there, but can be the endpoints of field lines.

Since there are an infinite number of points, an infinite number of field lines can be drawn; but only a limited number can be shown on a field line diagram. Therefore which field lines are shown is a choice made by the person or computer program which draws the diagram, and a single vector field may be depicted by different sets of field lines. A field line diagram is necessarily an incomplete description of a vector field, since it gives no information about the field between the drawn field lines, and the choice of how many and which lines to show determines how much useful information the diagram gives.

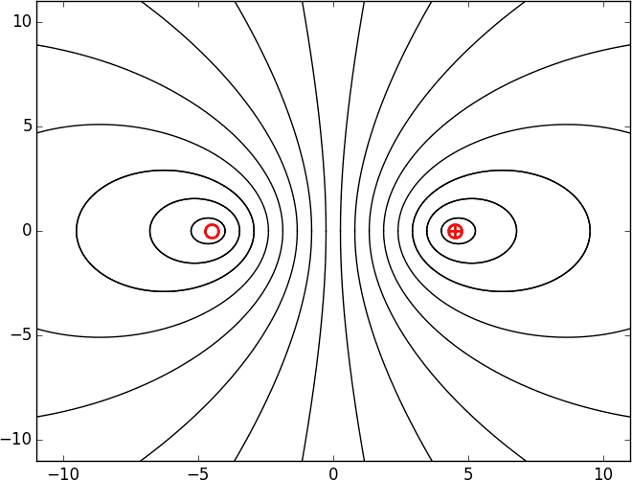
Field lines will have a start at the source of a vector field, where its divergence is positive. Field lines that go into the sink of a vector field, where divergence is negative, will there have their end. Field lines can also form closed loops, or extend to or from infinity, or continue forever without closing in on themselves.^[4][5] An individual field line shows the direction of the vector field but not the magnitude. In order to also depict the magnitude of the field, a selection of field lines can be drawn such that the density of field lines (number of field lines per unit perpendicular area) at any location is proportional to the magnitude of the vector field at that point. Areas in which neighboring field lines are converging (getting closer together) indicates that the field is getting stronger in that direction.

In physics, drawings of field lines are mainly useful in cases where the sources and sinks, if any, have a physical meaning, as opposed to e.g. the case of a force field of a radial harmonic. For example, Gauss's law states that an electric field has sources at positive charges, sinks at negative charges, and neither elsewhere, so electric field lines start at positive charges and end at negative charges. A gravitational field has no sources, it has sinks at masses, and it has neither elsewhere, gravitational field lines come from infinity and end at masses. A magnetic field has no sources or sinks (Gauss's law for magnetism), so its field lines have no start or end: they can only form closed loops, extend to infinity in both directions, or continue indefinitely without ever crossing itself. However, as stated above, a special situation may occur around points where the field is zero (that cannot be intersected by field lines, because their direction would not be defined) and the simultaneous begin and end of field lines takes place. This situation happens, for instance, in the middle between two identical positive electric point charges. There, the field vanishes and the lines coming axially from the charges end. At the same time, in the transverse plane passing through the middle point, an infinite number of field lines diverge radially. The concomitant presence of the lines that end and begin preserves the divergence-free character of the field in the point.^[5]

Note that for this kind of drawing, where the field-line density is intended to be proportional to the field magnitude, it is important to represent all three dimensions. For example, consider the electric field arising from a single, isolated point charge. The electric field lines in this case are straight lines that emanate from the charge uniformly in all directions in three-dimensional space. This means that their density is proportional to ${\displaystyle 1/r^2}$, the correct result consistent with Coulomb's law for this case. However, if the electric field lines for this setup were just drawn on a two-dimensional plane, their two-dimensional density would be proportional to ${\displaystyle 1/r}$, an incorrect result for this situation.^[6]

Construction[edit]

Given a vector field ${\displaystyle \mathbf{F}(\mathbf{x})}$ and a starting point ${\displaystyle {\mathbf{x}}_{\text{0}}}$ a field line can be constructed iteratively by finding the field vector at that point ${\displaystyle \mathbf{F}({\mathbf{x}}_{\text{0}})}$. The unit tangent vector at that point is: ${\displaystyle \mathbf{F}({\mathbf{x}}_{\text{0}})/|\mathbf{F}({\mathbf{x}}_{\text{0}})|}$. By moving a short distance ${\displaystyle ds}$ along the field direction a new point on the line can be found

${\displaystyle {\mathbf{x}}_{\text{1}}={\mathbf{x}}_{\text{0}}+\frac{\mathbf{F}({\mathbf{x}}_{\text{0}})}{|\mathbf{F}({\mathbf{x}}_{\text{0}})|}ds}$

Then the field at that point ${\displaystyle \mathbf{F}({\mathbf{x}}_{\text{1}})}$ is found and moving a further distance ${\displaystyle ds}$ in that direction the next point ${\displaystyle \mathbf{F}({\mathbf{x}}_{\text{2}})}$ of the field line is found. At each point ${\displaystyle {\mathbf{x}}_{\text{i}}}$ the next point can be found by

${\displaystyle {\mathbf{x}}_{\text{i+1}}={\mathbf{x}}_{\text{i}}+\frac{\mathbf{F}({\mathbf{x}}_{\text{i}})}{|\mathbf{F}({\mathbf{x}}_{\text{i}})|}ds}$

By repeating this and connecting the points, the field line can be extended as far as desired. This is only an approximation to the actual field line, since each straight segment isn't actually tangent to the field along its length, just at its starting point. But by using a small enough value for ${\displaystyle ds}$, taking a greater number of shorter steps, the field line can be approximated as closely as desired. The field line can be extended in the opposite direction from ${\displaystyle {\mathbf{x}}_{\text{0}}}$ by taking each step in the opposite direction by using a negative step ${\displaystyle -ds}$.

Examples[edit]

If the vector field describes a velocityfield, then the field lines follow stream lines in the flow. Perhaps the most familiar example of a vector field described by field lines is the magnetic field, which is often depicted using field lines emanating from a magnet.

Divergence and curl[edit]

Field lines can be used to trace familiar quantities from vector calculus:

• Divergence may be easily seen through field lines, assuming the lines are drawn such that the density of field lines is proportional to the magnitude of the field (see above). In this case, the divergence may be seen as the beginning and ending of field lines. If the vector field is the resultant of radial inverse-square law fields with respect to one or more sources then this corresponds to the fact that the divergence of such a field is zero outside the sources. In a solenoidal vector field (i.e., a vector field where the divergence is zero everywhere), the field lines neither begin nor end; they either form closed loops, or go off to infinity in both directions. If a vector field has positive divergence in some area, there will be field lines starting from points in that area. If a vector field has negative divergence in some area, there will be field lines ending at points in that area.
• The Kelvin–Stokes theorem shows that field lines of a vector field with zero curl (i.e., a conservative vector field, e.g. a gravitational field or an electrostatic field) cannot be closed loops. In other words, curl is always present when a field line forms a closed loop. It may be present in other situations too, such as a helical shape of field lines.

Physical significance[edit]

While field lines are a 'mere' mathematical construction, in some circumstances they take on physical significance. In fluid mechanics, the velocity field lines (streamlines) in steady flow represent the paths of particles of the fluid. In the context of plasma physics, electrons or ions that happen to be on the same field line interact strongly, while particles on different field lines in general do not interact. This is the same behavior that the particles of iron filings exhibit in a magnetic field.

The iron filings in the photo appear to be aligning themselves with discrete field lines, but the situation is more complex. It is easy to visualize as a two-stage-process: first, the filings are spread evenly over the magnetic field but all aligned in the direction of the field. Then, based on the scale and ferromagnetic properties of the filings they damp the field to either side, creating the apparent spaces between the lines that we see.^{[citation needed]} Of course the two stages described here happen concurrently until an equilibrium is achieved. Because the intrinsic magnetism of the filings modifies the field, the lines shown by the filings are only an approximation of the field lines of the original magnetic field. Magnetic fields are continuous, and do not have discrete lines.

See also[edit]

• External ray — field lines of Douady–Hubbard potential of Mandelbrot set or filled-in Julia sets

References[edit]

1. ^ ^abTou, Stephen (2011). Visualization of Fields and Applications in Engineering. John Wiley and Sons. p. 64. ISBN9780470978467.
2. ^ ^abcDurrant, Alan (1996). Vectors in Physics and Engineering. CRC Press. pp. 129–130. ISBN9780412627101.
3. ^ ^abHaus, Herman A.; Mechior, James R. (1998). 'Section 2.7: Visualization of Fields and the Divergence and Curl'. Electromagnetic fields and energy. Hypermedia Teaching Facility, Massachusetts Institute of Technology. Retrieved 9 November 2019.
4. ^Lieberherr, Martin (6 July 2010). 'The magnetic field lines of a helical coil are not simple loops'. American Journal of Physics. 78 (11): 1117–1119. Bibcode:2010AmJPh..78.1117L. doi:10.1119/1.3471233.
5. ^ ^abZilberti, Luca (25 April 2017). 'The Misconception of Closed Magnetic Flux Lines'. IEEE Magnetics Letters. 8: art. 1306005 – via Zenodo (https://zenodo.org/record/4518772#.YCJU_WhKjIU).
6. ^A. Wolf, S. J. Van Hook, E. R. Weeks, Electric field line diagrams don't work Am. J. Phys., Vol. 64, No. 6. (1996), pp. 714–724 DOI 10.1119/1.18237

Further reading[edit]

• Griffiths, David J. (1998). Introduction to Electrodynamics (3rd ed.). Prentice Hall. pp. 65–67 and 232. ISBN978-0-13-805326-0.

External links[edit]

Wikimedia Commons has media related to Field diagrams.

• Interactive Java applet showing the electric field lines of selected pairs of charges by Wolfgang Bauer
• 'Visualization of Fields and the Divergence and Curl' course notes from a course at the Massachusetts Institute of Technology.

In our homes, cars, communications, computing and machinery, electric currents are are usually channeled by insulation wrapped around wires and boundaries.

On the other hand, mapping the structure of the Earth's magnetism across continents and oceans makes one think of effects spread out in space. Both channeled and unbounded phenomena exist and have their uses: information can be spread by both insulated telegraph wires and freely propagating radio waves. Two names stand out in the study of spread-out electric and magnetic phenomena in the 19th century: the Englishman Michael Faraday and the Scot James Clerk Maxwell--one an intuitive observer, the other a gifted mathematical scientist.

Michael Faraday was born in England In 1791, to the family of a blacksmith. His formal education stopped early, after which he was apprenticed to a bookbinder, providing cheap labor in return to learning a trade (Ben Franklin was similarly apprenticed to his brother, a printer). As books came to the shop to be rebound, Michael found opportunities to read them. Among them was a volume of the Encyclopaedia Britannica, summing up what was then known about electricity.

Anothe bright light of British science in the early 1800s was Humphry Davy, who 'lived in the odium/of having discovered sodium.' He did so by passing an electric current through molten table salt NaCl; salt dissolved in water would not do, because there, any molecule of NaCl broken up would break up a water molecule H₂0 , create NaOH and HCl, and these would recombine to give again NaCl. He similarly separated potassium from its salt Kcl, also invented the extremely bright electric arc lamp, also a safety lantern for coal miners and more.

Not too long before that, the USA gained its independence from Britain, and one supporter of the crown in that war ('tory') was Benjamin Thompson of Rumford, near Boston. Thompson had to flee to England and later acquired the title 'Count Rumford' in the service of a German prince. With some scientists, Rumford founded the 'Royal Institution' in London for promoting science in Britain, and Davy gave there popular public lectures on the world of science. (The Royal Institution still exists, and now includes--among others--a museum devoted to Faraday).

Faraday managed to attend the lectures and kept detailed notes. When Davy fired an assistant for brawling, Faraday--now older--applied for the position, sending along his notebook as evidence of earnestness. He was hired, rose to become Davy's secretary and prime assistant, and in later years, his rival.

Magnetic Field Lines

Faraday's main asset was his clear intuition, reflected in his lucid style in writing and lecturing. He also excelled in chemistry, kept detailed notebooks and was active in the Sandemanian church. To visualize magnetic forces, he imagined space around a magnet filled with a huge bundle of lines each of which, like a drawn arrow, had a definite direction, giving at any point the local direction of magnetic force. That is, the direction in which the north-seeking pole ('N pole') of a freely suspended compass needle would point, and in which a free-floating magnetic N-pole would be pushed by magnetic forces. He named them magnetic lines of force, though nowadays 'magnetic field lines' is the usual term.

With the Earth's north-south magnetic force, these lines fan out from the vicinity of the south magnetic pole, arch above the (magnetic) equator and converge again in the region around the northern magnetic pole.

Lines of latitude and longitude on Earth are just a visualization--one can be drawn through any point on Earth. Were magnetic field lines like that too (but in three dimensions)? Faraday was not sure--a space filled with magnetic field lines did not seem to him empty any more.

This ambiguity still persists. Yes, they are just a visualization, pure mathematical abstractions. But they are also uniquely useful, in applications such as labeling the motion of electrons in space near a magnet. They seem to give only the direction of the magnetic force, not its strength--but their global configuration allows strength to be deduced, since they cluster more densely wherever the magnetic force is stronger. A related concept, 'magnetic flux,' is extremely useful in designing machinery (and will come up in a later section). And yes, space around electric currents and charges, as we see it today, is not really empty but has specific properties (such as energy density). Today we call such modified space a 'field'--a magnetic field, electric field or electromagnetic field. Many of these ideas started with Faraday's 'lines of force,' though (as discussed later) they were also foreshadowed by the study of fluids.

'Magnetic Rotations'

As Oersted demonstrated, an electric current in a wire also created magnetic forces, but in that case the field lines were closed loops around the current flow

Fieldline Pro Series

. Since compass needles tend to line up in the direction of the local field line, this explained why Oersted observed them trying to become oriented perpendicular to the wire. Field lines also trace the force on an isolated magnetic N-pole. Such isolated poles do not exist, but it is possible to observe forces on them if the corresponding S-pole is far enough to be hardly affected. In 1821, after Oersted had published his findings, Faraday (possibly with Davy's advice) devised a clever experiment to do so.

In a goblet filled with mercury--a dense metal liquid at room temperature and conducting electricity--Faraday immersed a long iron bar magnet (iron floats in mercury). One end of the magnet (say, the S-pole end) was tied flexibly to a hook at the bottom, while the other floated up at an angle, poking out near the rim of the goblet. A vertical metal rod held by a stand poked into the middle of the goblet (left image below) and connected to one side of a 'voltaic pile' electric battery, while the other side was electrically connected to the mercury. When the circuit was closed, a current flowed through the rod, creating loops of field lines, and the floating N-pole end of the magnet circled around them.

The S-pole in this case was tied down in one place, which served as pivot to the rotation. Reversing the battery connections reversed the rotation, as did exchanging the positions of the magnetic poles.

By Newton's 3rd law of mechanics, all forces act symmetrically: whenever the current exerts a force on a magnetic pole, the pole exerts an opposite and equal force on the current. This allowed Faraday to demonstrate the reverse process as well: the magnet was now vertically fixed along the axis of the goblet (right-hand image), while the rod conducting the current hung at an angle from a supporting stand, its tip floating near the edge of the goblet. This time, when the battery was connected, it was the rod that rotated around a cone. In a way, these were the first electric motors--though not very efficient ones, since the currents they required were rather large.

From experiments like this, Faraday devised his 'right hand rule': stretch your right hand thumb and bend the other four fingers. If the thumb points in the direction of the current, the fingers curl in the direction in which field lines go around the wire.

Fieldline Range Bag